Мерзляк Геометрія 7 клас

Вправа 538

 

Умова:

У гострокутному трикутнику ABC проведено бісектрису ВМ. Із точки М на сторону ВС опущено перпендикуляр МК. Виявилося, що ∟ABM = ∟KMC. Доведіть, що трикутник ABC рівнобедрений.

 

Відповідь:

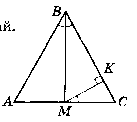
Нехай дано ∆АВС, ВМ - бісектриса, МК ┴ ВС. ∟ABM = ∟KMC.
Доведемо, що ∆АВС - рівнобедрений.
∟ABM = ∟MBC (ВМ - бісектриса ∟B).
∟ABM = ∟KMC, тоді ∟ABM = ∟KMC = ∟MBC = х.
Розглянемо ∆МКС (∟K = 90°). ∟KMC + ∟C = 90°; ∟C = 90° - х.
Розглянемо ∆ВМС.
∟MBC + ∟BMC + ∟C = 180°;
∟BMC = 180° - (90° - х + х) = 90°.
Розглянемо ∆АВС.
ВМ - бісектриса (за умовою), ВМ - висота (ВМ ┴ АС).
Тоді ∆АВС - рівнобедрений.