Геометрія 7 клас

Вправа 558

 

Умова:

Периметр трикутника ABC, описаного навколо кола, дорівнює 52 см. Точка дотику кола до сторони АВ ділить цю сторону у відношенні 2 : 3, рахуючи від вершини А. Точка дотику до сторони ВС віддалена від вершини С на 6 см. Знайдіть сторони трикутника.

 

Відповідь:

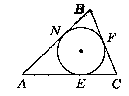
Дано:
Коло вписане у ∆АВС. N, Е, F - точки дотику.
Р_∆АВС = 52 см. AN : NB = 2 : 3. ЕС = 6 см. Знайти: АВ, ВС, АС.
Розв'язання:
За умовою AN : NB = 2 : 3, тоді AN = 2х (см), NB = 3х (см).
За властивістю дотичних, проведених до кола з однієї точки, маємо:
AN = AF = 2х (см), NB = BE = 3х (см), ЕС = FC = 6 см.
За аксіомою вимірювання відрізків маємо:
АВ = AN + NB; АВ = 2х + 3х = 5х (см).
ВС = BE + ЕС; ВС = 3х + 6 (см);
AC = AF + FC; АС = 2х + 6 (см). В = АВ + ВС + АС.
Складемо i розв'яжемо рівняння:
5х + 3х + 6 + 2х + 6 = 52; 10х + 12 = 52; 10х = 51 - 12; 10х = 40;
х = 40 : 10; х = 4. АВ = 5 • 4 = 20 (см); ВС = 3 • 4 + 6 = 18 (см);
АС = 2 • 4 + 6 = 14 (см).
Biдповідь: 20 см, 18 см, 14 см.