Геометрія 7 клас відповіді
Вправа 560
Умова:
Коло, вписане в рівнобедрений трикутник ABC, дотикається до його бічних cтopiн АВ i ВС у точках М i N відповідно. Доведіть, що MN ‖ AC.
Відповідь:
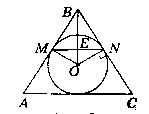
Дано:
∆АВС - рівнобедрений, АВ = ВС. О - центр вписаного кола у ∆АВС.
М, N - точки дотику, Довести: MN ‖ АС.
Доведения:
За умовою ∆АВС - рівнобедрений (АВ = ВС).
За властивістю кутів рівнобедреного трикутника маємо:
Нехай ∟A = х, ∟C = х.
За теоремою про суму кутів трикутника маємо:
∟ABC = 180° - 2х. О - центр вписаного кола, тоді ВО - бісектриса
∟MBN, тоді ∟MBO = ∟OBN = ∟MBN : 2.
∟МBO = ∟NBO = (180° - 2х) : 2 = 90° - х.
МО i NO - радіуси вписаного кола, тоді за властивістю дотичних
до кола маємо: ОМ ┴ AB, ON ┴ ВС.
Розглянемо ∆ОВМ i ∆ONB - прямокутні ∟OMB = ∟ONB = 90°,
ОМ = ON, OB - спільна сторона, тоді ∟MOE = ∟NOE.
Розглянемо ∆МОВ - прямокутний (∟B = 90°).
За властивістю гострих кутів прямокутного трикутника маємо:
∟MOB = 90° - (90° - х) = 90° - 90° + х = х.
Отже, ∟MOE = ∟NOE = х; ∟MON = 2х.
∆MON - рівнобедрений (ОМ = ON).
За властивістю кутів рівнобедреного трикутника маємо:
∟OMN = ∟ONM = (180° - 2х) : 2 = 90° - х.
За аксіомою вимірювання кутів маємо: ∟EMB = ∟OMB - ∟OME.
∟EMB = 90° - (90° - х) = 90° - 90° + х = х.
Отже, ∟A = ∟EMB = х (відповіднв).
За ознакою паралельності прямих маємо: AC ‖ MN, АВ - січна.
Доведено.
Повідомити про помилку
Обгрунтуй, що саме не так!




