Мерзляк домашня з геометрії 7 клас решебник відповіді гдз
Вправа 561
Умова:
Доведіть, що коли центр кола, описаного навколо трикутника, належить його стороні, то цей трикутник - прямокутний.
Відповідь:
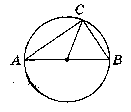
Дано:
∆АВС, О - центр описаного кола, О є АС.
Довести: ∆АВС - прямокутний.
Доведения:
Нехай ∟C = х. Розглянемо ∆СОВ - рівнобедрений (ОС = ОВ - радіуси).
За властивістю кутів рівнобедреного трикутника маємо: ∟C = ∟OBC = х.
За теоремою про суму кутів трикутника маємо:
∟BOC = 180° - (х + х) = 180° - 2х. ∟AOB i ∟BOC - суміжні.
За теоремою про суміжні кути маємо:
∟AOB = 180° - (180° - 2х) = 180° - 180° + 2х = 2х.
Розглянемо ∆АОВ - рівнобедрений (АО = ОВ - радіуси).
∟OAB = ∟OBA = (180° - 2х) : 2 = 90° - х.
За аксіомою вимірювання кутів маємо:
∟ABC = ∟ABO + ∟OBC, ∟ABC = (90° - х) + х = 90°.
Тобто ∟ABC = 90°, тоді ∆АВС - прямокутний.
Доведено.
Повідомити про помилку
Обгрунтуй, що саме не так!




