Геометрія 7 клас
Вправа 562
Умова:
У трикутник ABC вписано коло, яке дотикається до сторони АВ у точці М, ВС = а. Доведіть, що AM = р - а, де р - півпериметр трикутника ABC.
Відповідь:
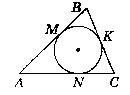
Дано:
∆АВС, О - центр вписаного кола. М - точка дотику, М є АВ, ВС = а.
Довести: AM = р - а.
Доведения:
За властивістю дотичних, проведених до кола з однієї точки, маємо:
AM = AN, BM = ВК, СК = CN. AN = AM.
Р = АВ + ВС + АС. АВ = AM + MB, ВС = ВК + КС, АС = AN + NС.
Р = AM + MB + ВК + КС + AN + NC;
P = 2(ВК + КС + AM);
р = ВК + КС + AM; р = ВС + AM; AM = р - а.
Доведено.
Повідомити про помилку
Обгрунтуй, що саме не так!




