Мерзляк домашня з геометрії 7 клас відповіді

Вправа 563

 

Умова:

До кола, вписаного в рівносторонній трикутник зi стороною а, проведено дотичну, яка перетинає дві сторони трикутника. Знайдіть периметр трикутника, який ця дотична відтинає від даного.

 

Відповідь:

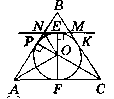
Дано:
∆АВС - рівносторонній, АВ - а, О - центр вписаного кола.
MN - дотична до кола, Знайти: P_∆NBM.
Розв'язання:
О - центр вписаного кола. За властивістю дотичних до кола маємо:
ОЕ ┴ NM, OP ┴ АВ.
О - центр вписаного кола, СР - бісектриса, медіана.
Отже, АР = РВ = 1/2АВ; АР = РВ = а/2.
NO - бісектриса ∟РОЕ; ∟PON = ∟NOE = ∟POE : 2.
АО - бісектриса. ∟РАО = ∟FAO = 60° : 2 = 30°.
∟APO = 90° - 30° = 60°; ∟AOF = 60°; ∟POF = 60° + 60° = 120°;
∟POE = 180° - 120° = 60° (∟FOP i ∟POE - суміжні).
∟PON = ∟NOE = 60° : 2 = 30°.
∆NEO - прямокутний (∟E = 90°), ∟NOE = 90°.
За властивістю катета, який лежить навпроти кута 30° маємо: NE = 1/2NO.
За властивістю дотичних, проведених до кола з однієї точки, маємо:
PN = NE = 1/2NO.
Розглянемо ∆ONB - рівнобедрений (ON = NB). ∟EON = ∟NBE = 30°;
NO = NB.
Нехай NE = NP = x, тоді NB = 2x; PB = PN + NB; PB = x + 2x = 3x.
PB = а/2; 3x = а/2; x = а/6; 2x = а/3. ∆NBM - piвносторонній.
P_∆NBM = 3 • NB = 3 • 2х = 3 • а/3 = а.
Biдповідь: a.