Геометрія 7 клас гдз

Вправа 564

 

Умова:

У рівнобедрений трикутник ABC (АВ = ВС) з основою 10 см вписано коло. До цього кола проведено три дотичні, які відтинають від даного трикутника трикутники ADK, BEF i CMN. Сума периметрів утворених трикутників дорівнює 42 см. Чому дорівнює бічна сторона даного трикутника?

 

Відповідь:

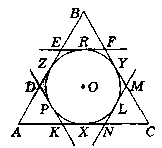
Дано:
∆АВС - рівнобедрений, АВ = ВС. О - центр вписаного кола, АС = 10 см.
Р_∆АDК + Р_∆NМС + Р_∆ЕВF = 42 см. Знайти: АВ.
Розв'язання:
За властивістю дотичних, проведених до кола з однієї точки, маємо:
КР = КХ, XN = NL, LM = MY, YF = FR,
RE = EZ, ZD = DP.
KN = KX + XN, NM = NL + LM, MF = MY + YE, FE = FR + RE,
DE = DZ + ZD, DK = DP + PK.
Звідси маємо:
KN + FM + ED = NM + FE + ZК.
АВ + ВС + AC = (AD + DE + EB) + (BF + FM + MC) + (AK + KN + NC) =
= (BE + BF) + (CM + CN) + (AK + AD) + (DE + FM + КN) =
= (BE + BF) + (CM + CN) + (AK + AD) + (ZK + FE + NM) =
= (BE + BF + EF) + (CM + CN + MN) + (AK + AD + DK) =
= Р∆АDК + Р∆NМС + Р∆ЕВF = 42 cм.
AC = 10 см, 2АВ + 10 = 42; 2AB = 42 - 10 = 32; AC = 16 см.
Biдповідь: 16 см.