Геометрія 7 клас Мерзляк решебник відповіді гдз
Вправа 566
Умова:
Кожний iз кутів ВАС i АСВ трикутника ABC поділено на три piвні частини (рис. 309). Доведіть, що ∟AMN = ∟CMN.
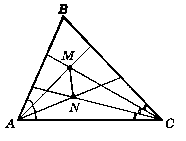
Відповідь:
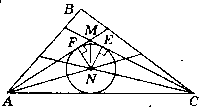
Дано:
∆АВС. ∟BAC поділено на три piвні кути, ∟BCA поділено на три piвнi кути.
Довести: ∟AMN = ∟CMN.
Доведения:
Розглянемо ∆АМС. AN - бісектриса ∟MAC, CN - бісектриса ∟MCA.
Отже, N - центр кола, вписаного у ∆АМС.
Е, F - точки дотику вписаного кола зi сторонами AM i МС.
За властивістю дотичних, проведених до кола, маємо: NE ┴ МС, NF ┴ AM.
Розглянемо ∆MNE i ∆NFM - прямокутні.
∟NFM = ∟NEM = 90°, FN = EN - радіуси вписаного кола, MN - спільна сторона.
Отже, ∆NFM = ∆NEM (за ознакою piвностi прямокутних трикутників).
Звідси маемо: ∟FMN = ∟EMN, тобто ∟AMN = ∟CMN.
Доведено.
Повідомити про помилку
Обгрунтуй, що саме не так!




