Мерзляк домашня з геометрії 7 клас відповіді гдз

Вправа 632

 

Умова:

У трикутнику ABC відомо, що ∟C = 90°. На катеті АС побудите точку D, яка віддалена від прямої АВ на вiдстань CD.

 

Відповідь:

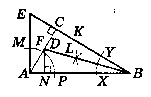
Дано:
∆АВС - прямокутний.
∟C = 90°.
Побудувати: на АС точку D; CD = DM. DM ┴ АВ.
Побудова:
Якщо точка D повинна бути віддалена від гіпотенузи АВ на відстань CD, тому DM ┴ AB. DM = DC.
Отже, D - повинна бути центром кола вписаного у трикутник ABE, AC - бісектриса ∟EAB.
∟CAB = ∟CAE.
Тобто треба побудувати ∆ЕАВ на ocновi сторони АВ, кута В, та кута
∟ЕАВ, який удвічі більший за ∟CAB.
Тобто спочатку треба побудувати на сторот AC ∟EAC = ∟CAB.
1) Будуємо коло з центром в точці А довільного радіуса.
2) Коло перетинає сторону АВ в точці Р i сторону АС в точці F.
3) Вимірюємо циркулем довжину відрізку PF.
4) Будуємо дугу з центром в точці F радіусом FP.
5) Точку перетину двох дуг позначаємо М.
6) Будуємо промінь AM.
7) Будуємо промінь ВС.
8) Позначаємо точку перетину променів AM i ВС Е.
Отримали ∆ЕАВ.
Щоб знайти центр кола вписаного у ∆АВЕ, треба побудувати бісектрису ∟B.
1) Будуємо коло з центром в точці В довільного радіуса.
2) Це коло перетинає сторону АВ в точці X, сторону ВС в точці У.
3) Будуємо коло довільного радіуса з центром в точці X.
4) Будуємо коло того ж радіуса з центром в точці У.
5) Позначаємо точку перетину цих кіл L.
6) Будуємо промінь BL, який перетинає сторону АС в точці D.
7) D - центр кола, вписаного у ∆АВЕ.
Отже, DC = DM (DM ┴ АВ). За властивістю дотичних до кола.