Мерзляк Геометрія 7 клас

Вправа 646

 

Умова:

Побудуйте прямокутний трикутник за гіпотенузою та сумою катетів.

 

Відповідь:

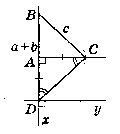
Дано: гіпотенуза с, сума катетів а + b.
Побудувати прямокутний трикутник за гіпотенузою с та сумою катетів а + b.
Побудова:
1) Будуємо довільну пряму х.
2) Позначаємо на прямій довільну точку В.
3) Вимірюємо циркулем довжину відрізку, який дорівнює cyмi катетів а + b.
4) Будуємо дугу з центром в точці В i радіусом а + b.
Точка перетину прямої i дуги позначаємо D.
5) Через точку D проводимо пряму у, перпендикулярну до прямої а (b ┴ а).
6) Будуємо бісектрису прямого кута D.
7) Вимірюємо циркулем довжину відрізку с (гіпотенузи).
8) Будуємо дугу з центром в точці В i радіусом с.
9) Точка перетину бісектриси i дуги позначаємо С.
10) Проводимо через точку С перпендикуляр до прямої BD.
11) Позначаємо точку перетину відрізку BD i перпендикуляра А.
Отримали ∆CAD - рівнобедрений прямокутний (∟A = 90°; ∟D = 45°; тому ∟C = 45°).
Отже, AD = АС.
Отримали ∆BAC - прямокутний, у якому катети a i b та гіпотенуза с.