Мерзляк Геометрія 7 клас решебник відповіді гдз

Вправа 660

 

Умова:

На рисунку 334 ∟A = 46°, ∟ACB = 68°, ∟DEC = 120°. Знайдіть кути трикутників EFC i DBE.

 

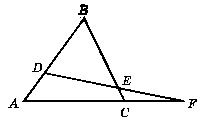
Відповідь:

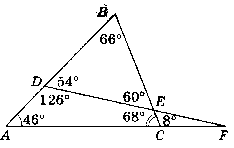
Дано: ∟A = 46°; ∟ACB = 68°; ∟DEC = 120°.
Знайти: кути ∆ЕFC i ∆DBE.
Розв'язання:
Розглянемо ∆АВС. За теоремою про суму кутів трикутника маємо:
∟A + ∟B + ∟ACE = 180°. ∟B = 180° - (46° + 68°) = 180° - 114° = 66°.
∟BED та ∟DEC - суміжні.
За теоремою про суміжні кути маємо:
∟BED + ∟DEC = 180°. ∟BED = 180° - 120° = 60°.
Розглянемо ∆DBE.
За теоремою про суму кутів трикутника маємо:
∟B + ∟BDE + ∟BED = 180°. ∟BDE = 180° - (66° + 60°) = 180° - 126° = 54°.
∟BDE i ∟EDA - суміжні. За теоремою про суміжні кути маємо:
∟BDE + ∟EDA = 180°. ∟EDA = 180° - 54° = 126°.
Розглянемо ∆FDA.
За теоремою про суму кутів трикутника маємо:
∟A + ∟F + ∟ADE = 180°. ∟F = 180° - (46° + 126°) = 180° - 172° = 8°.
Розглянемо ∆ECF.
∟ECF i ∟ECA - суміжні. Тобто ∟ECF + ∟ECA = 180°.
∟ECF = 180° - 68° = 112°. ∟CEF + ∟F + ∟ECF = 180°.
∟CEF = 180° - (8° + 112°) = 180° - 120° = 60°.
Biдповідь: кути ∆EFC: 60°; 8°; 112°; кути ∆DBE: 66°; 60°; 54°.