Геометрія 7 клас гдз

Вправа 662

 

Умова:

У трикутнику ABC з вершини прямого кута С проведено висоту СН i бісектрису СМ. Довжина відрізка НМ удвічі менша від довжини відрізка СМ. Знайдіть гострi кути трикутника ABC.

 

Відповідь:

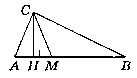
Дано: ∆АВС - прямокутний. ∟C = 90°.
СН - висота (СН ┴ АС). СМ - бісектриса ∟ACB.
НМ < СМ у 2 рази.
Знайти: ∟A; ∟B.
Розв'язання:
За умовою СН - висота (СН ┴ АВ), тобто ∟CHM = 90°.
Розглянемо ∟CHM - прямокутний (∟H = 90°).
Нехай НМ = х см, тоді СМ = 2х (см).
За властивістю катета, який лежить навпроти кута 30°, маємо: ∟HCM = 30°.
За умовою СМ - бісектриса ∟ACB.
За означенням бісектриси кута трикутника маємо:
∟ACM = ∟MCB = 1/2∟ACB = 90° : 2 = 45°.
За аксіомою вимірювання кутів маємо:
∟HCB = ∟HCM + ∟MCB; ∟HCB = 30° + 45° = 75°.
∟ACH = ∟ACM - ∟HCM; ∟ACH = 45° - 30° = 15°.
Розглянемо ∆CHA - прямокутний (∟H = 90°).
За властивістю гострих кутів прямокутного трикутника маємо:
∟CAH + ∟ACH = 90°; ∟CAH = 90° - 15° = 75°.
Аналогічно з ∆СНВ маємо: ∟CBH = 90° - 75° = 15°.
Biдповідь: 75°; 15°.