Геометрія 7 клас відповіді

Вправа 663

 

Умова:

На рисунку 335 BD = DC, DN ┴ ВС, ∟BDM = ∟MDA. Знайдіть суму кутів MBN та BMD.

 

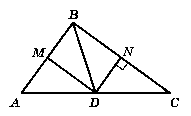
Відповідь:

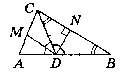
Дано: ∆АВС. BD = DC. DN ┴ ВС. ∟BDM = ∟MDA.
Знайти: ∟MBN + ∟BMD.
Розв'язання:
За умовою ВС = DC, отже ∆BDC - piвнобедрений.
За властивістю кутів рівнобедреного трикутника маємо: ∟DBN = ∟DCN. DN - висота (DN ┴ ВС).
За властивістю висоти в рівнобедреному трикутнику маємо: DN - медіана i бісектриса.
За означенням бісектриси кута маємо: ∟BDN = ∟NDC.
За аксіомою вимірювання кутів маємо:
∟ADC = ∟ADM + ∟MDB + ∟BDN + ∟NDC.
2∟MDB + 2∟BDN = 180°; 2(∟MDB + ∟BDN) = 180°.
∟MDB + ∟BDN = 90°; ∟MDN = ∟MDB + ∟BDN; ∟MDN = 90°.
Розглянемо ∆BND.
За теоремою про суму кутів трикутника маємо ∟BND + ∟NDB + ∟DBN = 180°.
Розглянемо ∆BMD.
Аналогічно маємо: ∟BMD + ∟MDB + ∟DBM = 180°.
Звідси маємо, що сума кутів чотирикутника BMDN дорівнюе 360°.
Отже, ∟BMD + ∟MDN + ∟DNB + ∟NBM = 360°.
Звідси маємо: ∟MBN + ∟BMD = 360° - (90° + 90°) = 360° - 180° = 180°.
Biдповідь: 180°.