Мерзляк Геометрія 7 клас

Вправа 671

 

Умова:

Градусні три суміжних кутів ABC i CBD відносяться як 5 : 4. Знайдіть кут між бісектрисами кутів ABC i ABD. Скільки розв'язків має задача?

 

Відповідь:

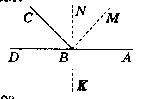
Нехай ∟ABC i ∟CBD - суміжні. ∟ABC : ∟CBD = 5 : 4.
BM - бiceктриса ∟CBA, BN - бісектриса ∟ABD.
Знайдемо ∟NBM.
∟ABC + ∟CBD = 180° (як суміжні).
∟ABC = 180° : (5 + 4) • 5 = 100°,
∟CBD = 180° - 100° = 80°.
∟CBM = ∟MBA = 1/2∟CBA = 100° : 2 = 50°.
∟ABD - розгорнутий. ∟DBN = ∟NBA = 180° : 2 = 90°.
∟NBA = ∟NBM + ∟MBA, 90° = ∟NBM + 50°, ∟NBM = 90° - 50° = 40°.
Якщо бісектриса ∟ABD - BK, то ∟DBK = ∟KBA = 180° : 2 = 90°.
∟KBM = ∟KBA + ∟ABM, ∟KBM = 90° + 50° = 140°.
Biдповідь: 1) ∟NBM = 40°; 2) ∟KBM = 140°.