Геометрія 7 клас

Вправа 673

 

Умова:

На рисунку 338 BD ┴ ВС. Кут між бісектрисами кутів ABD i DBC дорівнює 55°. Знайдіть кут ABD.

 

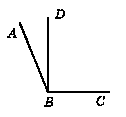
Відповідь:

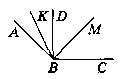
Нехай BD ┴ ВС, ВК - бісектриса ∟ABD, ВМ - бісектриса ∟DВС. ∟KBM = 55°.
Знайдемо ∟ABD.
Оскільки бісектриси ділять кути навпіл, то
∟ABK = ∟KBD, ∟DBM = ∟MBC.
∟KBM = ∟KBD + ∟DBM = 55° (за умовою).
∟ABK + ∟MBC = ∟KBM = 55°.
∟ABC = 55° • 2 = 110°.
Так як BD ┴ ВС, то ∟DBC = 90°.
∟ABC = ∟ABD + ∟DBC, ∟ABD = 110° - 90° = 20°.
Biдповідь: ∟ABD = 20°.