Геометрія 7 клас решебник відповіді гдз
Вправа 677
Умова:
У трикутниках ABC i DEF проведено медіани ВМ i ЕК відповідно. Відомо, що BC = EF, ∟ABC = ∟DEF, ∟C = ∟F.
Доведіть, що: 1) ∆ВМС и ∆EFK; 2) ∆АВМ = ∆DEK.
Відповідь:
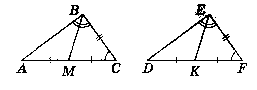
Дано: ∆АВС i ∆DEF. ВМ i ЕК - медіани. ВС = EF; ∟C = ∟F. ∟АВС = ∟DEF.
Довести: 1) ∆ВМС = ∆EFK.
Доведения:
Розглянемо ∆АВС i ∆DEF.
За умовою ∟АВС = ∟DEF, ∟C = ∟F та СВ = EF.
За II ознакою piвностi трикутників маємо: ∆АВС = ∆DEF.
Звідси маємо: АС = DF.
За умовою ВМ - медіана. За означенням медіани маємо: AM = МС.
Аналогічно ЕК - медіана, тоді DK = KF.
Отже, AM = МС = DK = KF.
Розглянемо ∆ВМС i ∆EKF.
ВС = EF, МС = AT; ∟C = ∟F.
Отже, за I ознакою piвностi трикутників маємо: ∆ВМС = ∆EKF; ∆ВМС ≠ ∆EFK.
Доведено.
Довести: 2) ∆АВМ - ∆DEK.
Доведення:
Як довели раніше ∆АВС = ∆DEF. Звідси маємо: АВ = DЕ; ∟A = ∟D.
Розглянемо ∆АВМ i ∆DEК. АВ = DE; AM = DK; ∟A = ∟D.
За I ознакою piвностi трикутників маємо: ∆АВМ = ∆DEK.
Доведено.
Повідомити про помилку
Обгрунтуй, що саме не так!




