Геометрія 7 клас

Вправа 680

 

Умова:

У трикутниках ABC i DEF відомо, що AC = DF, ВС = EF, ∟C = ∟F. Бісектриси кутів ВАС i ABC перетинаються в точці О, а бісектриси кутів DEF i EDF - у точці М. Доведіть, що ∆AOB = ∆DME.

 

Відповідь:

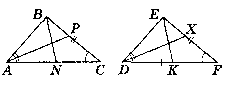
Дано: ∆АВС i ∆DEF. AC = DF; ВС = EF; АР - бісектриса ∟ВАС;
BN - бісектриса ∟ABC; BN ∩ AP = О; EK - бісектриса ∟DEF.
DX - бісектриса ∟EDF. DX ∩ EK = M.
Довести: ∆AOB = ∆DME.
Доведения:
Розглянемо ∆АВС i ∆DEF.
За умовою АС = DF; ВС = EF; ∟С = ∟F.
За I ознакою piвностi трикутників маємо: ∆АВС = ∆DEF.
Звідси маємо АВ = DE, ∟ВАС = ∟EDK, ∟АВС = ∟DEF.
За умовою АР - бісектриса ∟ВАС.
За означенням бісектриси кута маємо:
∟ВАО = ∟OAN = 1/2∟ВАС.
Аналогічно АХ - бісектриса ∟EDF. Звідси маємо:
∟EDM = ∟MDK = 1/2∟EDF. Отже, ∟ВАО = ∟EDM.
BN - бісектриса ∟ABC, тоді ∟АВО = ∟ОВС = 1/2∟АВС.
ЕК - бісектриса ∟DEF, тоді ∟DEM = ∟MEF.
Отже, ∟ABO = ∟DEM.
Розглянемо ∆АВО i ∆DEM.
AB = DE; ∟ABO = ∟DEM, ∟BAO = ∟EDM.
За II ознакою piвностi трикутників маємо: ∆АОВ = ∆DME.
Доведено.