Геометрія 7 клас решебник

Вправа 683

 

Умова:

На рисунку 340 АВ = ВС, AD = FC, ∟ADE = ∟CFE. Доведіть, що точка Е - середина відрізка АС.

 

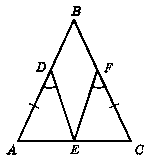
Відповідь:

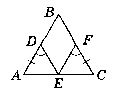
Дано: ∆АВС. АВ = ВС, AD = FC. ∟ADE = ∟CFE.
Довести: Е - середина АС.
Доведення:
За умовою АВ - ВС, тоді ∆АВС - рівнобедрений.
За властивістю кутів рівнобедреного трикутника маємо: ∟A = ∟C.
Розглянемо ∆ADE i ∆EFC.
За умовою AD = FC, ∟ADE = ∟EFC та ∟A = ∟C.
За II ознакою piвностi трикутників маємо: ∆ADE = ∆CFE.
Звідси маємо: АЕ = ЕС, отже, Е - середина АС.
Доведено.