з геометрії 7 клас відповіді
Вправа 684
Умова:
Рівнобедрені трикутники ABC i ADC мають спільну основу АС. Доведіть, що пряма BD - серединний перпендикуляр відрізка АС.
Відповідь:
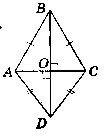
Дано: ∆АВС - рівнобедрений, АС - основа. ∆ADC - рівнобедрений, АС - основа.
Довести: BD - серединний перпендикуляр до АС.
Доведення:
Розглянемо ∆АВС - рівнобедрений (АВ = ВС).
Проведемо ВО - висоту ВО ┴ АС.
За властивістю рівнобедреного трикутника маємо: ВО - медіана, АО = ОС.
Розглянемо ∆ADC - рівнобедрений (AD = DC).
Проведемо DO ┴ AC.
За властивістю висоти рівнобедреного трикутника маємо: DO - медіана, АО = ОС.
ВО ┴ АС i DO ┴ АС, тоді BD ┴ AC i О - середина АС.
Отже, BD - серединний перпендикуляр до АС.
Доведено.
Повідомити про помилку
Обгрунтуй, що саме не так!




