Мерзляк Геометрія 7 клас гдз

Вправа 687

 

Умова:

Точка О - точка перетину серединних перпендикуляpiв сторін AC i ВС трикутника ABC - належить його стороні АВ. Доведіть, що: 1) точка О - середина відрізка АВ; 2) ∟ACB = ∟A + ∟B.

 

Відповідь:

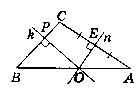
Дано: ∆АВС; n - серединний перпендикуляр
до сторони АС; Е - середина AC; к - серединний перпендикуляр до СВ,
Р - середина ВС; k ∩ n = 0. О є АВ.
Довести: 1) О - середина АВ.
Доведення:
За умовою k - серединний перпендикуляр до сторони ВС i
n - серединний перпендикуляр до сторони АС.
За умовою k ∩ n = 0.
О - центр описаного кола, тобто серединний перпендикуляр до
сторони ВА проходить через точку О. Отже, О - середина ДА.
Доведено.
Довести: 2) ∟ACB = ∟A + ∟B.
Доведення:
Як відомо, центр описаного кола навколо прямокутного трикутника
належить гіпотенузі, тобто, якщо О є АВ, тоді АВ - гіротенуза.
Звідси маємо: ∆АВС - прямокутний; ∟ACB = 90°.
За властивістю гострих кутів прямокутного трикутника маємо:
∟A + ∟B = 90°. Тобто, ∟ACB = ∟A + ∟B.
Доведено.