Мерзляк Геометрія 7 клас
Вправа 688
Умова:
Медіана трикутника ABC розбиває його на два трикутники, периметри яких piвнi. Доведіть, що трикутник ABC рівнобедрений.
Відповідь:
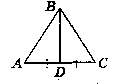
Дано; ∆АВС; BD - медіана; Р∆АВD = P∆ВCD.
Довести: ∆АВС - рівнобедрений.
Доведення:
BD - медіана.
За означенням медіани трикутника маємо:
D - середина АС, отже, AD = DC.
За умовою Р∆АВD = P∆ВCD.
P∆АВD = AB + BD + AD.
Р∆ВСD = BC + CD + BD.
BD - спільна сторона.
AB + BD + AD = ВС + BD + DC (DC = AD).
AB + BD + AD - BD - AD = ВС.
AB = ВС, тобто ∆АВС - рівнобедрений.
Доведено.
Повідомити про помилку
Обгрунтуй, що саме не так!




