Геометрія 7 клас

Вправа 690

 

Умова:

На сторонах AC i ВС трикутника ABC позначено точки F i К відповідно. Доведіть, що коли трикутники AFB i АКВ рівні, а сторони АК i BF відповідні, то трикутник ABC рівнобедрений.

 

Відповідь:

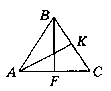
Дано: ∆АВС. F є АС; К є ВС. ∆АКВ = ∆AFB (AK i BF відповідні).
Довести: ∆АВС - рівнобедрений.
Доведення:
За умовою ∆АВК = ∆BAF. Звідси маємо: ∟BAF = ∟ABK.
За властивістю кутів при ocнові piвнобедреного трикутника маємо:
∆АВС - рівнобедрений (АВ - основа).
Доведено.