Геометрія 7 клас решебник гдз
Вправа 691
Умова:
На рисунку 343 AM = CN, AB = CD, BN = DM. Доведіть, що ∟ABN = ∟CDM.
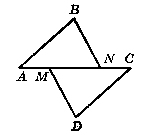
Відповідь:
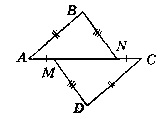
Дано: AM = CN; AB = CD; BN = DM.
Довести: ∟ABN = ∟CDM.
Доведення:
Розглянемо ∆ABN i ∆CDM.
За умовою AB = CD, BN = DM, AC = NC.
За аксіомою вимірювання відрізків маємо:
AN = AM + MN, MC = MN + NC. MN - спільна сторона.
За III ознакою piвностi трикутників маємо: ∆ABN = ∆СDМ.
Звідси маємо: ∟ABN = ∟CDM.
Доведено.
Повідомити про помилку
Обгрунтуй, що саме не так!




