Мерзляк Якір Геометрія 7 клас

Вправа 694

 

Умова:

На сторонах АВ i АС трикутника ABC позначили відповідно точки М i K так, що ∟AMK = ∟ABC. Доведіть, що ∟AKM = ∟ACB.

 

Відповідь:

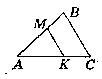
Нехай ∆АВС - даний, т. М лежить на АВ, т. К лежить на AC, ∟AMK = ∟ABC.
Доведемо, що ∟AKM = ∟ACB.
Розглянемо пряму МК i ВС та січну АВ.
∟AMK i ∟ABC - відповідні, оскільки за умовою вони piвнi, то МК ‖ ВС.
Розглянемо МК ‖ ВС i ciчнy AC. ∟АКМ = ∟ACB - як відповідні.