Мерзляк Геометрія 7 клас решебник

Вправа 698

 

Умова:

На продовженні бічних сторін AC i ВС рівнобедреного трикутника ABC за вершину С позначено точки Е i D відповідно так, що DE ‖ AB. Доведіть, що трикутник CDE рівнобедрений.

 

Відповідь:

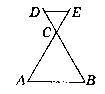
Нехай даний ∆АВС - рівнобедрений (АС = ВС), DE ‖ АВ.
Доведемо, що ∆CDE - рівно6едрений.
Розглянемо DE ‖ АВ, АЕ - січна. ∟DEC = ∟BAC (як різносторонні).
Розглянемо DE ‖ АВ, BD - січна. ∟EDC = ∟ABC (як різносторонні).
Оскільки ∟CAB = ∟CBA (∆АВС - рівнобедрений), то ∟DEC = ∟EDC,
тоді ∆DEC - рівнобедрений.