Геометрія 7 клас
Вправа 703
Умова:
Пряма, паралельна стороні АС трикутника ABC, перетинає його сторони АВ i ВС у точках М і К відповідно так, що АМ = МК. Відомо, що ∟B = 65°, ∟C = 45°. Знайдіть кут КАС.
Відповідь:
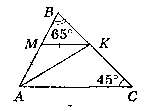
Нехай ∆АВС - даний, ∟В = 65°, ∟C = 45°, МК ‖ АС, МК = AM.
Знайдемо ∟KAC.
Розглянемо ∆АВС: ∟А = 180° - (∟B + ∟C), ∟A = 180° = (65° + 45°) = 180° - 110° = 70°.
МК ‖ АС, АВ - січна, тоді ∟BMK = ∟A = 70° (як відповідні).
∟BMK - зовнішній кут ∆АМК.
∟BMK = ∟MAK + ∟MKA, ∟MAK = ∟MKA (∆AMK - рівнобедрений (AM = MK)).
∟MAK = ∟MKA = 70° : 2 = 35°.
∟A = ∟MAK + ∟KAC, 70° = 35° + ∟KAC, ∟KAC = 70° - 35° = 35°.
Biдповідь: ∟KAC = 35°.
Повідомити про помилку
Обгрунтуй, що саме не так!




