Геометрія 7 клас відповіді

Вправа 710

 

Умова:

Висоти ВМ i СК трикутника ABC перетинаються в точці Н, ∟ABC = 35°, ∟ACB = 83°. Знайдіть кут ВНС.

 

Відповідь:

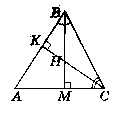
Нехай даний ∆АВС, ∟АВС = 35°, ∟АСВ = 83°, ВМ і СК -
висоти, перетинаються в т. Н. Знайдемо ∟ВНС.
Розглянемо ∆АВС.
∟А = 180° - (∟ABC + ∟АСВ),
∟А = 180° - (35° + 83°) = 62°.
Розглянемо ∆АВМ.
∟AMB = 90° (ВМ - висота),
∟ABM = 180° - (∟АМВ + ∟A), ∟ABM = 28°.
Розглянемо ∆КВС.
∟ВКС = 90° (СК - висота),
∟ВСК = 180° - (∟ВКС + ∟КВС),
∟ВСК = 55°, ∟ABC = 35°,
∟ABC = ∟ABM + ∟MBC, 35° = 28° + ∟MBC, ∟MBC = 7°.
Розглянемо ∆НВС.
∟НВС = 7°, ∟BCH = 55°,
∟ВНС = 180° - (∟HBC + ∟ВСН),
∟ВНС = 180° - (7° + 55°), ∟BHC = 180° - 62° = 118°.
Biдповідь: ∟ВНС = 118°.