Геометрія 7 клас

Вправа 712

 

Умова:

На гіпотенузі АВ прямокутного рівнобедреного трикутника ABC позначили точки М i К так, що АС = АМ i ВС = ВК. Знайдіть кут МСК.

 

Відповідь:

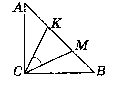
Нехай ∆АВС - прямокутний, рівнобедрений (АС = ВС).
АС = AM, ВС = ВК. Знайдемо ∟MCK.
Розглянемо ∆АВС.
∟C = 90°, ∟A = ∟B = 45°.
Розглянемо ∆АМС i ∆ВКС.
1) АС = ВС (∆АВС - рівнобедрений, АС = ВС).
2) Ат = ВК (за умовою).
3) ∟A = ∟B = 45°.
Отже, ∆АМС = ∆ВКС за I ознакою piвностi трикутників.
3 цього випливає, що ∟AMC = ∟ВКС.
Розглянемо ∆АМС - рівнобедрений (АС = AM).
∟ACM = ∟AMC = (182° - 45°) : 2 = 67,5°.
Розглянемо ∆СМК:
∟KMC = ∟CKM = 67,5°.
∟MCK = 180° - (∟KMC + ∟CKM),
∟MCK = 180° - (67,5° + 67,5°) = 45°.
Biдповідь: ∟MCK = 45°.