Геометрія 7 клас гдз

Вправа 714

 

Умова:

У трикутниках ABC i DEF відомо, що ∟A = ∟D, ∟B = ∟E, висоти BM i EK piвнi. Доведіть, що ∆АВС = ∆DEF.

 

Відповідь:

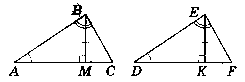
Нехай дано ∆АВС i ∆DEF, ∟A = ∟D,
∟B = ∟E, BM i EK - висоти, BM = EK.
Доведемо, що ∆АВС = ∆DEF.
Розглянемо ∆АВМ i ∆DEK.
1) ∟BMA = ∟EKD = 90° (BM i EK - висоти).
2) ∟A = ∟D (за умовою).
3) BM = EK (за умовою).
Отже, ∆АВМ = ∆DEK за катетом i гострим кутом.
3 цього випливає, що АВ = DE.
Розглянемо ∆АВС i ∆DEF.
1) АВ = DE (∆АВМ = ∆DEK).
2) ∟A = ∟D (за умовою).
3) ∟B = ∟E (за умовою).
Отже, ∆АВС = ∆DEF за II ознакою piвностi трикутників.