Мерзляк Геометрія 7 клас
Вправа 715
Умова:
Висоти AM i CK трикутника ABC перетинаються в точці О, ОК = ОМ, ∟BAM = ∟ACK. Доведіть, що трикутник ABC piвносторонній.
Відповідь:
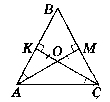
Нехай дано ∆АВС, AM i CK - висоти, т. О - точка перетину висот. ОК = ОМ, ∟ВАМ = ∟ACK.
Доведемо, що ∆АВС - рівносторонній.
Нехай ∟ВАМ = ∟АСК = х.
Розглянемо ∆АВМ (∟М = 90°). ∟В = 90° - х.
Розглянемо ∆КВС (∟К = 90°). ∟В = 90° - х, ∟ВСК = х.
Розглянемо ∆КОА i ∆МОС.
1) ∟OКА = ∟ОМС = 90° (АМ i CK - висоти).
2) КО = ОМ (за умовою).
3) ∟КAO = ∟MCO = х.
Отже, ∆КОА = ∆МОС за катетом i гострим кутом, з цього випливає,
що АО = ОС. Тоді ∆АОС - рівнобедрений i ∟ОАС = ∟ОСА = х.
Розглянемо ∆АВС.
∟В = 90° - х, ∟А = х + х = 2х, ∟С = х + х = 2х.
Оскільки ∟А + ∟В + ∟С = 180°, то 90 - х + 2х + 2х = 180;
90 + 3х = 180; 3х = 90; х = 30.
∟В = 90° - 30° = 60°, ∟А = 30° + 30° = 60°,
∟С = 30° + 30° = 60°.
Якщо в ∆АВС ∟А = ∟В = ∟С = 60°, то цей трикутник - рівносторонній.
Повідомити про помилку
Обгрунтуй, що саме не так!




