Геометрія 7 клас Мерзляк решебник відповіді гдз

Вправа 716

 

Умова:

Дві висоти рівнобедреного трикутника при перетині утворюють кут 100°. Знайдіть кути даного трикутника.

 

Відповідь:

 

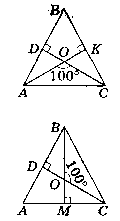
I випадок.
Розв'язання:
Нехай даний ∆АВС - рівнобедрений (АВ = ВС), висоти проведені iз кутів A i С.
АК i CD - висоти, т. О - точка їx перетину, ∟АОС = 100°.
Знайдемо кути ∆АВС.
∟DOA = ∟AOC = 180° (як суміжні).
∟DOA = 180° - 100° = 80°. ∟DOA = ∟КОС = 80° (як вертикальні).
Розглянемо ∆АВК. ∟AKB = 90°, ∟DAO = ∟KCO = 180° - (90° + 80°) = 10°,
∟ВАК = 10°, тоді ∟АВК = 90° - 10° = 80°.
Розглянемо ∆АВС - рівнобедрений, ∟В = 80°.
∟ВАС = ∟ВСА = (180° - 80°) : 2 = 50°.
Biдповідь: ∟В = 80°, ∟ВАС = ∟ВСА = 50°.

II випадок.
Розв'язання:
Нехай висоти ВМ i CD проведені відповідно з т. В i т. С.
∟BOD + ∟ВОС = 180° (як cyміжнi). ∟BOD = 180° - 100° = 80°.
Розглянемо ∆ВОD. ∟D = 90°, ∟DBO = 90° - ∟DOB,
∟DBO = 90° - 80° = 10°.
Розглянемо ∆АВС (АВ = ВС). ВМ - висота, проведена до основи,
тоді ВМ - бісектриса. ∟ABC = 2 • 10° = 20°, ∟А = ∟С = (180° - 20°) : 2 = 80°.
Biдповідь: ∟В = 20°, ∟А = ∟С = 80°.