з геометрії 7 клас гдз
Вправа 720
Умова:
У рівносторонньому трикутнику ABC iз середини М стороны АС опущено перпендикуляр МК на сторону ВС. Знайдіть периметр трикутника ABC, якщо КС = 3 см.
Відповідь:
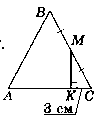
Нехай ∆ABC - рівносторонній, т. М - середина АС. МК ┴ АС, КС = 3 см.
Знайдемо Р∆ABC.
Оскільки ∆АВС - рівносторонній, то ∟A = ∟В = ∟C = 60°.
Розглянемо ∆MКС.
∟МКС = 90° (МК ┴ ВС). ∟C = 60°. ∟МКС = 90° - 60° = 30°.
В прямокутному трикутнику катет, що лежить напроти кута 30°,
дорівнює половит гіпотенузи КС = 1/2МС.
МС = 3 • 2 = 6 см, AM = МС = 6 см (т. М - середина АС).
АС = 2 • 6 = 12 см, АВ = АС - ВС = 12 см.
Р∆ABC = 3 • 12 = 36 см.
Biдповідь: Р∆ABC = 35 см.
Повідомити про помилку
Обгрунтуй, що саме не так!




