Мерзляк Полонський Геометрія 7 клас решебник відповіді

Вправа 724

 

Умова:

Знайдіть кут між прямими, на яких лежать дві медіани рівностороннього трикутника.

 

Відповідь:

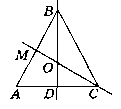
Нехай ∆АВС - рівносторонній, CM i BD - медіани, О - точка їx перетину.
Знайдемо кут між прямими BD i СМ.
BD - медіана, бісектриса i висота.
СМ - мед1ана, бкектриса i висота.
∟A = ∟B = ∟С = 60° (∆АВС - piвносторонній).
∟ABD = 1/2∟B = 60° : 2 = 30°. ∟CMB = 90° (CM - висота).
Розглянемо ∆ВМО:
∟BMO = 90°, ∟MBO = 30°, тоді ∟MOB = 60°.
∟MOB i є кутом між прямими BD i СМ.
Biдповідь: ∟MOB = 60°.