Мерзляк домашня з геометрії 7 клас решебник відповіді

Вправа 727

 

Умова:

У колі iз центром О проведено непаралельні хорди МК i NP, МК = NP, точки A i В - середини хорд МК i NP відповідно. Доведіть, що ∟OAB = ∟OBA.

 

Відповідь:

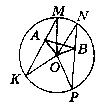
Дано: О - центр кола. KM, NP - хорди (KM не паралельне NC).
КМ = ND. А - середина КМ. В - середина NP.
Довести: ZOAB = ZOBA.
Доведення:
Виконаємо додаткові побудови: радіуси ОК, ОМ, ON, OP.
Розглянемо ∆КОМ i ∆NОР.
КО = ОМ та N0 = ОР - радіуси, тобто КО = N0 = ОМ = ОР (за побудовою).
За умовою КМ = NP.
За III ознакою piвностi трикутників маємо: ∆КОМ = ∆NOP.
Звідси маємо: ∟OKM = ∟OPN, ∟OMK = ∟ONP.
За умовою А - середина КМ, отже, КА = КМ = 1/2КМ.
В - середина NP, отже, BN = ВР = 1/2NP.
Розглянемо ∆АОК i ∆ОРВ.
Якщо АК = РВ; OK = OP, ∟OKM = ∟OPN.
За I ознакою piвностi трикутників маємо: ∆ОАК = ∆ОВР.
Звідси маємо: ОА = ОВ.
Тобто ∆ОАВ - р1внобедрений.
За властивістю кутів при основi piвнобедреного трикутника маємо: ∟OAB = ∟OBA.
Доведено.