Геометрія 7 клас гдз

Вправа 737

 

Умова:

Доведіть, що хорда кола, яка перпендикулярна до іншої хорди цього кола та проходить через її середину, є діаметром даного кола.

 

Відповідь:

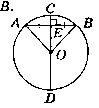
Дано: коло; АВ, CD - хорди. АВ ┴ CD; Е - середина АВ.
Довести: CD - діаметр.
Доведення:
Розглянемо ∆АОВ.
За умовою ОЕ ┴ АВ, ОЕ - висота, Е - середина АВ, ОЕ - медіана.
За властивістю рівнобедреного трикутника маємо: ∆АОВ - рівнобедрений.
АО = ОВ. Звіси маємо: О - центр кола. CD проходить через точку О,
отже, CD - діаметр.
Доведено.