Геометрія 7 клас відповіді
Вправа 738
Умова:
У колі проведено діаметр АВ i хорди АС та BD такі, що АС ‖ BD. Доведіть, що відрізок CD - діаметр кола.
Відповідь:
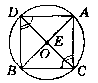
Дано: коло з центром в точці О; АС, BD - хорди; AC ‖ BD; АВ - діаметр.
Довести: CD - діаметр.
Доведення:
Виконаємо додаткову побудову: хорди AD i ВС.
Розглянемо ∆АВС. Якщо О є АВ, тоді ∆BAC - прямокутний (∟ACB = 90°).
Аналогічно ∆ADB - прямокутний (∟ADB = 90°). Нехай ∟ACD = х.
За аксіомою вимірювання кутів маємо: ∟АСВ = ∟ACD + ∟DCB; ∟DCB = 90° - х.
За умовою AC ‖ BD; CD - січна.
За ознакою паралельності прямих маємо:
∟ACD = ∟CDB = х (внутрішні разносторонні).
Розглянемо ∆DBC.
За теоремою про суму кутів трикутника маємо: ∟DCB + ∟CBD + ∟BDC = 180°.
∟CBD = 180° - (∟DCB + ∟BDC); ∟CBD = 180° - (x + 90° - x) = 90°.
Отже, ∆DBC - прямокутний (∟DBC = 90°).
Отже, О є DC. Якщо О є АВ; О є DC, де О - центр кола,
тоді АВ ∩ DC = 0, тобто DC - діаметр.
Доведено.
Повідомити про помилку
Обгрунтуй, що саме не так!




