Мерзляк Геометрія 7 клас

Вправа 740

 

Умова:

Коло, вписане в трикутник ABC, дотикається до його сторін АВ, ВС i АС у точках К, М і Е відповідно, АК = ВМ = СЕ. Доведіть, що трикутник ABC рівносторонній.

 

Відповідь:

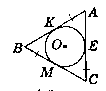
Дано: ∆АВС. О - центр кола, вписаного у ∆АВС.
К, Е, М - точки дотику. К є АВ; М є ВС; Е є АС.
АК = ВМ = СЕ.
Довести: ∆АВС - рівносторонній.
Доведення:
За властивістю дотичних, проведених до кола з однієї точки маємо:
АК = АЕ; СЕ = СМ; ВМ = ВК.
Отже, АК = KB = ВМ = МС = СЕ = АЕ.
Звідси маемо: АК + KB = ВМ + МС = СЕ + АС. АВ = ВС = АС,
тобто ∆АВС - piвносторонній.
Доведено.