з геометрії 7 клас решебник відповіді гдз

Вправа 741

 

Умова:

Бісектриси AD i СЕ трикутника ABC перетинаються в точці О₁, бісектриси EF i DK трикутника DEB перетинаються в точці О₂. Доведіть, що точки В, О₁ i О₂ лежать на одній прямій.

 

Відповідь:

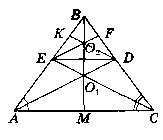
Дано: ∆АВС. AD i СЕ - бісектриси ∆АВС.
AD ∩ CE = О1, EF i DK - бісектриси ∆KBF.
EF ∩ DK = О2.
Довести: В, О1, О2 належать одній прямій.
Доведення:
За умовою AD i СЕ - бісектриси кутів ∆АВС.
AD ∩ CE = О₁, тобто О1 - є центром кола вписаного у ∆АВС;
ВМ - проходить через т. О1, ВМ є бісектрисою ∆АВС.
За умовою DK i EF - бісектриси кутів ∆DBE.
EF ∩ DK = О2, тобто О2 - є центром кола, вписаного у ∆EBD;
ВМ - бісектриса ∟ABC (∟ABC = ∟EBD).
Отже, ВМ проходить через т. О2.
Звідси маемо: В є ВМ, О1 є ВМ, О2 є ВМ.
Точки В, О1, О2 належать одній прямій.
Доведено.