Мерзляк Математика 6 клас

Вправа 1346

Умова:

Накресліть квадрат ABCD зі стороною 1 см та проводіть його діагоналі АС і BD. Через точки В і D проведіть прямі, перпендикулярні до прямої ВD, а через А і С - прямі, паралельні прямій ВD. Знайдіть точки перетину проведених прямих. Визначте вид многокутника, вершинами якого є ці точки, та знайдіть його площу.

 

Відповідь:

 

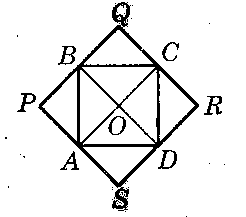
Отриманий чотирикутник PQRS - квадрат.
ABQC = АВОС, АВРА = АВОА, ADSA = ADOA, ADRC = ADOC.
Отже, площа квадрата PQRS удвічі більша за площу квадрата ABCD, тобто дорівнює 2 • 1 см² = 2 см².
Відповідь. 2 см².