Мерзляк домашня з геометрії 7 клас решебник гдз

Вправа 168

 

Умова:

На рисунку 139 АВ ┴ BD, CD ┴ BD, точка О - середина відрізка BD. Доведіть, що ∆АВО = ∆CDO.

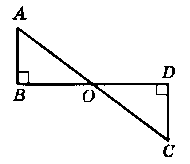
Відповідь:

Доведения: Розглянемо ∆АВО i ∆CDO.
1) ВО = OD (так як т. О - середина BD);
2) ∟ABO = ∟CDO = 90° (за умовою);
3) ∟AOB = ∟COD (як вертикальні).
Отже, ∆АВО = ∆CDO за II ознакою piвності трикутників.