Мерзляк Геометрія 7 клас решебник

Вправа 173

 

Умова:

Через точку М, яка належить бісектрисі кута з вершиною в точці О, проведено пряму, яка перпендикулярна до цієї бісектриси. Ця пряма перетинає сторони даного кута в точках A i В. Доведіть, що AM = MB.

 

Відповідь:

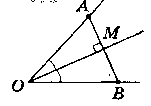
Доведения: Нехай дано ∟O, ОМ - бісектриса ∟O. АВ ┴ ОМ.
Розглянемо ∆АМО i ∆BMO. 1) ∟AOM = ∟BOM (ОМ - бісектриса ∟O);
2) ∟AMO = ∟BMO = 90° (за умовою);
3) ОМ - спільна.
Отже, ∆АМО = ∆ВМО за II ознакою, тому AM = MB.