Мерзляк Полонський Геометрія 7 клас

Вправа 177

 

Умова:

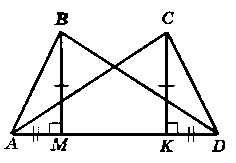
На рисунку 146 ВМ ┴ AD, СК ┴ AD, ВМ = СК, AM = KD. Доведіть, що ∆ABD = ∆CDA.

 

Відповідь:

Доведення:
Розглянемо ∆АВМ i A∆DCK.
1) ВМ = СК (за умовою);
2) AM = KD (за умовою);
3) ∟AMB = ∟DKC = 90° (так як ВМ ┴ AD, СК ┴ AD).
Отже, ∆АВМ = ∆DCK за I ознакою.
Розглянемо ∆ABD i ∆DCA.
1) AВ = CD (так як ∆АВМ = ∆DCK);
2) ∟BAD = ∟CDA (так як ∆АВМ = ∆DCK);
3) AD - спільна. Отже, ∆ABD = ∆DCA.