Геометрія 7 клас

Вправа 178

 

Умова:

Доведіть, що бісектриси рівних трикутників, проведені з вершин відповідних кутів, piвні.

 

Відповідь:

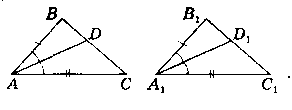
Доведения:
Нехай ∆АВС = ∆A₁B₁C₁.
AD - 6iceктриса ∟A,
A₁D₁ - бісектриса ∟A₁.
Доведемо, що AD = A₁D₁.
Розглянемо ∆ADC і ∆A₁D₁С₁
1) AC = A₁C₁ (так як ∆АВС = ∆A1B1C1);
2) ∟DCA = ∟D₁C₁A₁ (так як ∆АВС = ∆A1B1C1);
3) ∟DАC = 1/2∟A (AD - бісектриса ∟A);
∟D₁А₁C₁ = 1/2∟A (A₁D₁ - бісектриса ∟A₁).
Так як ∟A = ∟A₁ (∆ABC = ∆A1B1C1), то ∟DAC = ∟D₁А₁C₁.
Отже, ∆ADC = ∆A₁D₁C₁, тоді AD = A₁D₁.