з геометрії 7 клас

Вправа 297

 

Умова:

Точка В належитъ прямій АС, промені BD i BF лежать у різних півплощинах відносно прямої AC, ∟ABD = 80°, ∟ABF = 150°, ВМ - бісектриса кута DBF. Знайдіть кут МВС.

 

Відповідь:

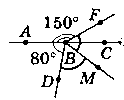
Дано:
пряма АС, В є AC; BF i BD лежать у різних півплощинах.
∟ABD = 80°, ∟ABF = 150°. ВМ - бісектриса ∟DBF.
Знайти: ∟МВС.
Розв'язання:
∟АВС - розгорнутий, ∟АВС = 180°.
За аксіомою вимірювання кутів маємо
∟АВС = ∟ABF + ∟FBC; ∟FBC = 180° - 150° = 30°.
Аналогічно, ∟АВС = ∟ABD + ∟DBC.
∟ВВС = 180° - 80° = 100°; ∟DBF = ∟DBC + ∟CBF; ∟DBF = 100° + 30° = 130.
За умовою ВМ - бісектриса ∟DBF.
За означениям бісектриси кута маємо
∟DBM = ∟MBF = 130° : 2 = 65°;
∟FBM = ∟FBC + ∟CBM, ∟СВМ = 65° - 30° = 35°.
Biдповідь: 35°.