Мерзляк Геометрія 7 клас відповіді

Вправа 343

 

Умова:

На рисунку 236 ∟MAB = 50°, ∟ABK = 130°, ∟ACB = 40°, СЕ - бісектриса кута ACD. Знайдіть кути трикутника АСЕ.

 

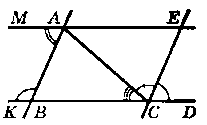
Відповідь:

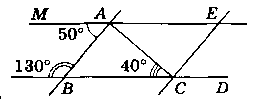
Дано:
∟MAB = 50°; ∟ABK = 130°;
∟ACB = 40°; СЕ - бісектриса ∆ACD.
Знайти: кути ∆АСЕ.
Розв'язання:
∟MAB i ∟KBA - внутрішні односторонні.
∟MAB + ∟KBA = 130° + 50° = 180°.
Тому за ознакою паралельності прямих маємо:
ME ‖ КС; АВ - січна; ME ‖ КС; АС - січна;
∟BCA = ∟CAE (внутрішні piзностороннi) ∟CAE = 40°.
∟BCA i ZACD - суміжні.
За теоремою про cyміжнi кути маємо:
∟BCA + ∟ACD = 180°. ∟ACD = 180° - 40° = 140°.
За умовою СЕ - бісектриса ∟ACD.
Тоді за означенням бісектриси кута маємо:
∟ACE = ∟ECD = 140° : 2 = 70°.
МК ‖ BD; СЕ - січна; ∟AEC = ∟DЕС = 70° (внутрішні різносторонні).
Biдповідь: 40°; 70°; 70°.