Геометрія 7 клас

Вправа 348

 

Умова:

На рисунку 240 АВ ‖ DE. Доведіть, що ∟BCD = ∟АВС + ∟CDE.

 

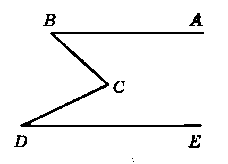
Відповідь:

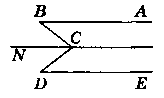
Дано:
АВ ‖ DE.
Довести: ∟BCD = ∟ABC + ∟CDE.
Доведения:
Виконаємо додаткову побудову: проведемо через точку С пряму
CN паралельну прямим АВ i DE (CN ‖ АВ; CN ‖ DE).
За аксіомою вимірювання кутів маємо:
∟BCD = ∟BCN + ∟NCD. ВА ‖ NC; ВС - січна.
За ознакою паралельності прямих маємо:
∟АВС = ∟BCN (внутрішні різносторонні).
Аналогічно CN ‖ DE, CD - січна.
∟NCD = ∟CDE (внутрішні різносторонні).
Тому ∟BCD = ∟ABC + ∟CDE.
Доведено.