Геометрія 7 клас відповіді гдз
Вправа 369
Умова:
У трикутнику ABC відомо, що ∟C = 90°, АК - бісектриса, ∟ВАК = 18°. Знайдіть кути АКС i ABC.
Відповідь:
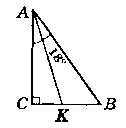
Нехай дано ∆АВС (∟C = 90°), АК - бісектриса ∟A, ∟BAK = 18°.
Знайдемо ∟AKC i ∟ABC.
∟BAK = ∟KAC = 18° (АК - бісектриса). ∟CAB = 2 • 18° = 36°.
В ∆АВС: ∟C + ∟CAB + ∟ABC = 180°. ∟ABC = 180° - (90° + 36°) = 54°.
Розглянемо ∆АСК (∟C = 90°), ∟KAC = 18°, тоді ∟AKC = 90° - 18° = 72°.
Biдповідь: ∟AKC = 72°; ∟ABC = 54°.
Повідомити про помилку
Обгрунтуй, що саме не так!




