Мерзляк Геометрія 7 клас гдз
Вправа 387
Умова:
Доведіть, що коли два кути одного трикутника дорівнюють відповідно двом кутам другого трикутника, то й треті кути цих трикутників piвнi.
Відповідь:
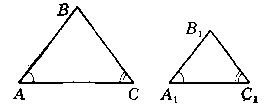
Доведення:
Нехай дано ∆АВС i ∆А1В1С1, ∟A = ∟A1; ∟C = ∟C1,
доведемо, що ∟B = ∟B1.
Розглянемо ∆АВС.
∟A + ∟B + ∟C = 180°.
∟B = 180° - (∟A + ∟C).
Розглянемо ∆А1В1С1: ∟A1 + ∟B1 + ∟C1 = 180°.
∟B1 = 180° - (∟A1 + ∟C1).
Оскільки ∟A = ∟A1 i ∟C = ∟C1,
то i ∟A + ∟C = ∟A1 + ∟C1, тоді ∟B = ∟B1.
Повідомити про помилку
Обгрунтуй, що саме не так!




