Геометрія 7 клас

Вправа 412

 

Умова:

Знайдіть кути трикутника ABC, якщо бісектриса кута В розбиває його на два рівнобедрених трикутники.

 

Відповідь:

 

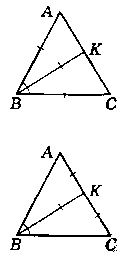
1) Нехай даний ∆АВС, ВК - бісектриса.
Припустимо, що ∆АВК - рівнобедрений (АВ = ВК),
∆АВС - рівнобедрений (ВК = ВС).
Розглянемо ∆АВС - рівнобедрений (АВ = ВС), тоді
бісектриса ВК є висотою i ∆АКВ = ∆СКВ = 90°.
Тоді в ∆АВК - рівнобедреному ∆АКВ = 90° при основі.
Це неможливо.
2) Нехай даний ∆АВС, ВК - бісектриса.
Припустимо, що ∆АКВ - рівнобедрений (АК = ВК),
∆ВКС - рівнобедрений (ВК = КС).
Нехай ∟ABK = ∟KBC = х (ВК - бісектриса).
∆АВК - рівнобедрений, тоді ∟АВК = ∟ВАК = х,
∆ВКС - рівнобедрений, тоді ∟КВС = ∟КСВ = х.
Розглянемо ∆АВС:
∟А = х, ∟В = 2х, ∟С = х; ∟А + ∟5 + ∟C = 180°;
х + 2х + х = 180; 4х = 180; х = 45.
∟А = 45°, ∟B = 90°, ∟C = 45°.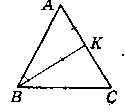

3) Нехай даний ∆АВС, ВК - бісектриса.
Припустимо, що ∆АКВ - рівнобедрений (АК = ВК),
∆ВАК - рівнобедрений (ВК = ВС).
Нехай ∟ABAT = ∟ATBC = х (ВК - бісектриса).
∆АВК - рівнобедрений, тоді ∟АВК = ∟ВАК = х,
∟АКВ = 180° - 2х. ∟AKB i ∟BKC - суміжні.
∟АКВ + ∟BKC = 180°. ∟AKB = 180° - ∟BKC, тоді ∟ВКС = 2х.
∆ВКС - рівнобедрений, тоді ∟BKC = ∟KCB = 2х.
Розглянемо ∆АВС: 
∟A = х, ∟В = 2х, ∟C = 2х. 
∟A + ∟В + ∟C = 180°.
х + 2х + 2х = 180°; 5х = 180; х = 36.
∟A = 36°. ∟B = 36° • 2 = 72°. ∟C = 36° • 2 = 72°.
Biдповідь: 90°, 45°, 45°; або 36°, 72°, 72°.