Мерзляк Якір Геометрія 7 клас решебник відповіді гдз

Вправа 504

 

Умова:

На стороні АВ трикутника ABC позначили точку М так, що ВМ = СМ, промінь МК - бісектриса кута АМС. Доведіть, що МК ‖ ВС.

 

Відповідь:

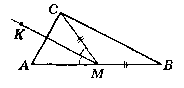
Дано:
∆АВС, М є АВ, СМ = MB.
МК - промінь, МК - бісектриса ∟AMC.
Довести: МК ‖ СВ.
Доведения'.
За умовою МК - бісектриса ∟AMC.
За означенням бісектриси трикутника маємо:
∟AMK = ∟KMC = 1/2∟AMC.
Нехай ∟AMK = ∟KMC = х, тоді ∟AMC = 2х. ∟AMC i ∟CMB - суміжні.
За теоремою про суміжні кути маємо: ∟CMB = 180° - 2х.
За умовою СМ = MB.
Отже, ∆СМВ - рівнобедрений.
За властивістю кутів рівнобедреного трикутника маємо:
∟MCB = ∟MBC = (180° - (180° - 2х)) : 2 =
= (180° - 180° + 2х) : 2 = (2х) : 2 = х.
Отже, ∟AMK = ∟MBC - х.
∟AMK i ∟MBC - відповідні.
Тому за ознакою паралельності прямих маємо: МК ‖ ВС, АВ - січна.
Доведено.